对数函数求导公式是怎么回事
说到对数函数求导,咱们先来个超简单的总结:自然对数 ln(x) 的导数是 1/x,而一般底数 a 的对数函数 log_a(x) 的导数其实就是 1/(x ln(a))。对,没错,就是这么简单又实用!这里有个小技巧哈,我们先用换底公式把 log_a(x) 换成 ln(x)/ln(a),然后因为 ln(a) 是个常数,导数计算时可以直接拿出来,当成系数来看待,剩下 ln(x) 的导数就是 1/x,最后把它们合起来就得到咱们那个经典的求导公式啦。如果你有点迷糊,别急,下面咱们接着聊聊具体是怎么一步步推导出来的。
其实这个公式也挺自然的:假设 y = log_a(x),那么咱们可以写成 x = a^y,这两个函数互为反函数。这是求导的大招——反函数求导法!对吧,你看,指数函数 a^y 的导数是 a^y ln(a),所以通过反函数求导定理,求 y = log_a(x) 的导数时,咱们直接用到这条关系。是不是听起来就很酷!
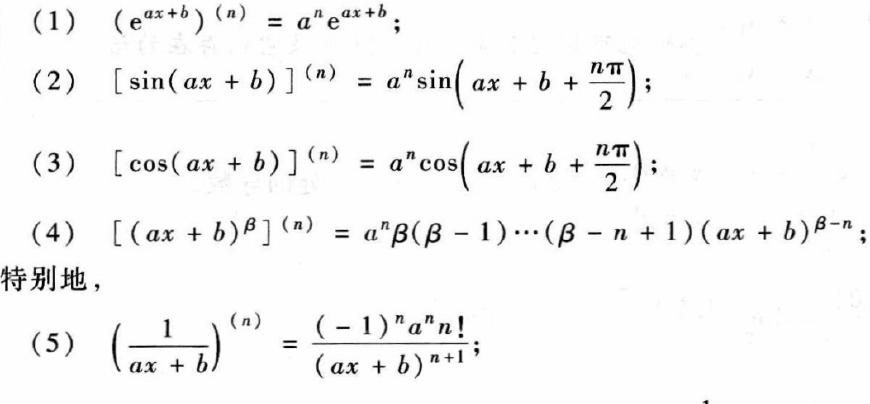
具体对数函数求导的方法有哪些
好啦,到了说方法的时候了,我们稍微分点条理,保证大家一看就懂:
-
利用换底公式
- 首先,log_a(x) = ln(x)/ln(a)
- 由于 ln(a) 是常数,求导时就是(1/ln(a))* (ln(x))'
- ln(x) 的导数是 1/x,所以整体就是 1/(x ln(a)) -
通过反函数求导关系
- 从 y = log_a(x) 变换到 x = a^y
- 对 x = a^y 求导,得 dx/dy = a^y ln(a)
- 利用反函数求导公式,dy/dx = 1 / (dx/dy) = 1/(a^y ln(a))
- 替换回 x,结果就是 dy/dx = 1/(x ln(a)) -
运用极限定义法
- 这是更原始的方式,用导数的极限形式去证明导数的结果
- 具体就是 lim(Δx→0) [log_a(x + Δx) - log_a(x)] / Δx
- 然后利用对数的性质和极限技巧,推导到同样的结果 -
注意底数和真数的限制
- 底数 a 必须大于0且不能等于1
- 真数 x 也要大于0,这样函数才定义的合理
- 这些限制非常重要,别忘了哦!
总的说,以上方法都很地道,各有侧重,懒得推导的宝宝就记公式,想透彻理解的可以试试反函数或者极限定义入门。学习求导其实挺有趣的,瞧见没,知识量大得让人“哇哦”!
相关问题解答
-
对数函数求导时为什么要用换底公式?
哎,这个问题棒呆啦!换底公式其实是个超级实用的小帮手,因为大部分系里和老师讲自然对数 ln(x) 求导最熟练(要知道它的导数1/x超简单!)。但是对数函数的底数 a 不同,怎么办?咱们就干脆把 log_a(x) 换成 ln(x)/ln(a),这样底数 a 变成了常数,轻轻松松用自然对数来做运算,简直就是化繁为简的典范,so easy! -
反函数求导法真的适用所有对数函数吗?
嘿嘿,几乎是啦!因为对数函数 y=log_a(x)和指数函数 x=a^y是反函数嘛,这玩意儿的求导大法宝就是“反函数求导定理”,它特别适合处理反函数的导数。所以你只要搞懂了指数函数的导数,求对数函数导数基本就没啥难度了,信不信由你,我觉得挺靠谱。 -
为什么底数 a 不能是1或者负数呢?
说实话,这其实是函数本身的定义问题。底数 a 必须大于0且不等于1,因为:
- 负数作为底数会导致对数定义域奇怪,值也不稳定,数学上不好用;
- 底数为1,1 的任何次方都等于1,根本没法建立一一对应关系,log_1(x)根本不定义。
说白了,这样规定是为了保证函数的良好性质和求导的合理性,so,不用纠结哦! -
求导的时候有什么小技巧可以更快算出来吗?
大招来了!平时你记住两个老兄:ln(x)导数是1/x,log_a(x)导数是1/(x ln(a)),遇到复杂点的你先把它换成ln的形式,这样看到导数的时候就不慌,感觉超级easy。而且多练习用反函数思想去推导,脑子能快速转起来,遇到新题目也不怕。关键是别忘了基础公式,熟能生巧嘛——听我的,天天练,你也能秒懂!

发表评论