说到矩阵的可约性,其实挺有意思的,就是看看一个矩阵能不能通过某些变换“化简”成更有结构的形式。简单来说,矩阵的约化过程是利用置换变换,把矩阵变成分块上三角矩阵。这一步听起来有点抽象,通俗点就是“把矩阵拆分成几个小模块”,这样做对于运算特别有帮助。
为什么要这么折腾呢?特别是对于对称的大型稀疏矩阵,经过约化后,可以极大加快矩阵的计算速度,操作起来事半功倍,效率真是高了好几个档次呢!所以,矩阵约化不仅是数学上的技巧,更是实际计算中的大帮手哦!
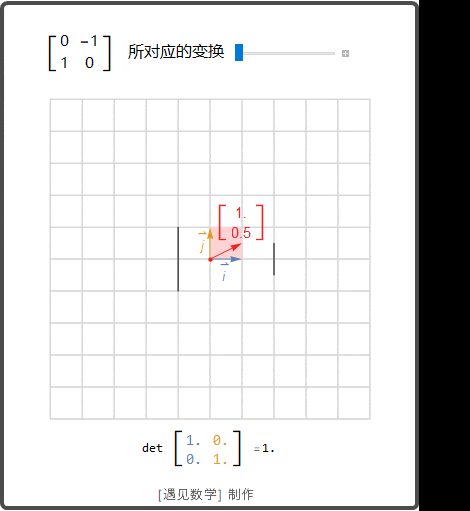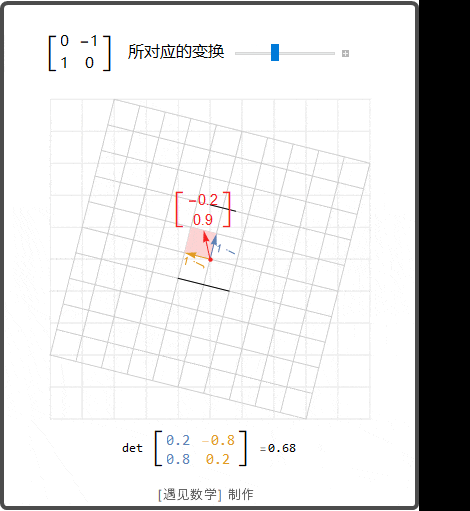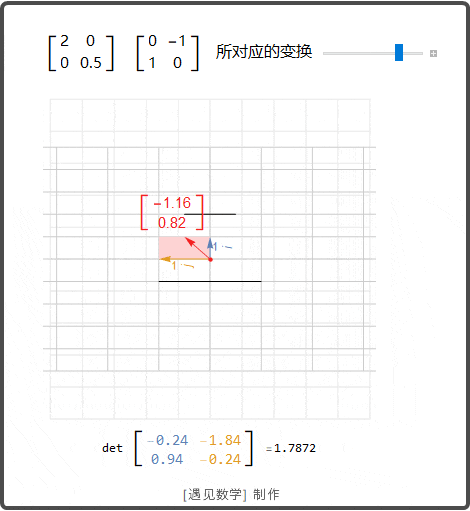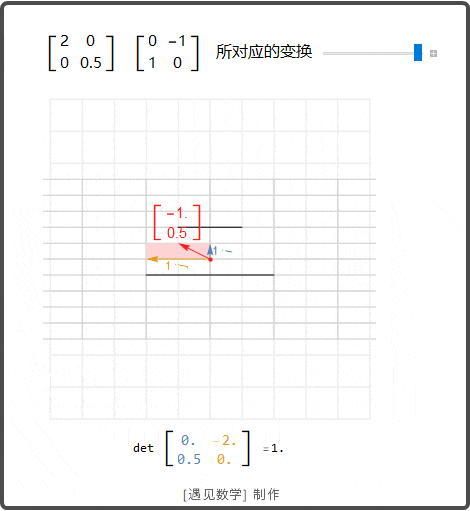
这块内容其实蛮多的,咱们来分点讲,方便理解:
多项式在有理数域上的可约性:
比如,多项式 ( x^4 - 4 ) 表面上看好像没啥有理根,但它在有理数域里是能拆开的!它可以写成 ((x^2 - 2)(x^2 + 2)),而这两个因子都是在有理数域上“不可约”的。也就是说,光凭有没有理根没法判断可约性,这点真是让人抓狂吧!
另外还有个超级实用的艾森斯坦判别法,就像数学界的“万能钥匙”,可以帮你判定很多多项式是否可约,非常nice!
全市可约的意思:
其实“全市可约”听起来高大上,但很简单,就是在整个市区范围内都能预约上,不管你在哪个区,服务都覆盖着,超级方便!如果某项服务标注“全市可约”,就表示你想预约啥,都能搞定,省心省力。
怎么认识同城可约的女孩子:
这儿提供几招实用的招数,帮你轻松认识同城的女孩子:
- 聊天技能是关键:聊啥聊得投其所好很重要,比如聊她喜欢的话题,分享趣味小故事,让聊天气氛变得轻松又有趣。
- 观察和模仿高手:看看那些聊天很溜的兄弟是怎么聊的,偷师学艺后用自己的方式去聊,别忘了真诚是超级无敌的加分项哦!
蝶恋声称的可约情况是否真实:
关于“蝶恋”的可约声称,咱们得擦亮眼睛。市面上确实有些平台或人,可能会夸大“可约”的真实性,甚至存在欺骗和诱导风险,比如骗钱或获取隐私啥的。虽然也不排除有些平台是合法合规的,但还是建议大家多留个心眼,避免着了坑,毕竟安全第一!

矩阵可约和不可约到底区别在哪儿呢?
哎呀,这问题问得棒棒哒!简单说,可约矩阵就像一块可以切成几块的小蛋糕,能变成分块上三角结构,而不可约矩阵是整块死死的、不好拆的蛋糕。这样分类其实是数学家们给矩阵排序的秘密武器,可以帮助我们节省计算时间,做题啊运算啥的都方便多了,太酷了!
为什么多项式有没有有理根不能简单判断可约性?
这事儿挺令人意外的!很多人以为只要有根就能拆开,没根就不行,其实不对。像 (x^4 - 4) 这个家伙,没有理根但竟然能拆!就是说,多项式的拆法不像买菜那么简单,不只靠找根,而是要用更高级的技巧,比如艾森斯坦判别法,真是让数学变得又神秘又有趣!
全市可约服务在现实中有啥实际好处?
哇,全市可约简直就是我们生活中的一大福音!不管你住在哪个角落,想啥服务都能预约上,省得到处跑找资源,这么一来做事特别省心又顺溜。关键是提高了效率,让时间和精力都能花在更重要的事情上,谁不喜欢呢,说到这我都激动了!
遇到社交平台上宣称可约的情况怎么办才安全?
这个问题超级关键!建议大家一定要谨慎对待这类信息,别被那些花里胡哨的文字忽悠了。先查查平台背景,看看有没有正经的认证和评价,再就是跟对方聊天时不要轻易泄露重要个人信息。说真的,天上不会掉馅饼,安全第一,小心驶得万年船嘛!
添加评论